题目描述

公元2044年，人类进入了宇宙纪元。

L 国有 \(n\) 个星球，还有 \(n-1\) 条双向航道，每条航道建立在两个星球之间，这 \(n-1\) 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司，该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从 \(u_i\) 号星球沿最快的宇航路径飞行到 \(v_i\) 号星球去。显然，飞船驶过一条航道是需要时间的，对于航道 \(j\)，任意飞船驶过它所花费的时间为 \(t_j\)，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新，L 国国王同意小 P 的物流公司参与 L 国的航道建设，即允许小 P 把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 \(m\) 个运输计划。在虫洞建设完成后，这 \(m\) 个运输计划会同时开始，所有飞船一起出发。当这 \(m\) 个运输计划都完成时，小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞，试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少？

输入

第一行，包括两个正整数 \(n,m\)，表示 L 国中星球的数量及小 P 公司预接的运输计划的数量，星球从 1 到 \(n\) 编号。

接下来 \(n-1\) 行描述航道的建设情况，其中第 \(i\) 行包含三个整数 \(a_i,b_i\) 和 \(t_i\)，表示第 \(i\) 条双向航道修建在 \(a_i\) 与 \(b_i\) 两个星球之间，任意飞船驶过它所花费的时间为 \(t_i\)。

接下来 \(m\) 行描述运输计划的情况，其中第 \(j\) 行包含两个正整数 \(u_j\) 和 \(v_j\)，表示第 \(j\) 个运输计划是从 \(u_j\) 号星球飞往 \(v_j\)号星球。数据保证 \(1 \leq u_i,v_i \leq n\)

输出

一个整数，表示小 P 的物流公司完成阶段性工作所需要的最短时间。

样例1

输入

6 3 
1 2 3 
1 6 4 
3 1 7 
4 3 6 
3 5 5 
3 6 
2 5 
4 5

输出

11

解释

将第 \(1\) 条航道改造成虫洞： 则三个计划耗时分别为：\(11, 12, 11\)，故需要花费的时间为 \(12\)。

将第 \(2\) 条航道改造成虫洞： 则三个计划耗时分别为：\(7, 15, 11\)，故需要花费的时间为 \(15\)。

将第 \(3\) 条航道改造成虫洞： 则三个计划耗时分别为：\(4, 8, 11\)，故需要花费的时间为 \(11\)。

将第 \(4\) 条航道改造成虫洞： 则三个计划耗时分别为：\(11, 15, 5\)，故需要花费的时间为 \(15\)。

将第 \(5\) 条航道改造成虫洞： 则三个计划耗时分别为：\(11, 10, 6\)，故需要花费的时间为 \(11\)。

故将第 \(3\) 条或第 \(5\) 条航道改造成虫洞均可使得完成阶段性工作的耗时最短，需要花费的时间为 \(11\)。

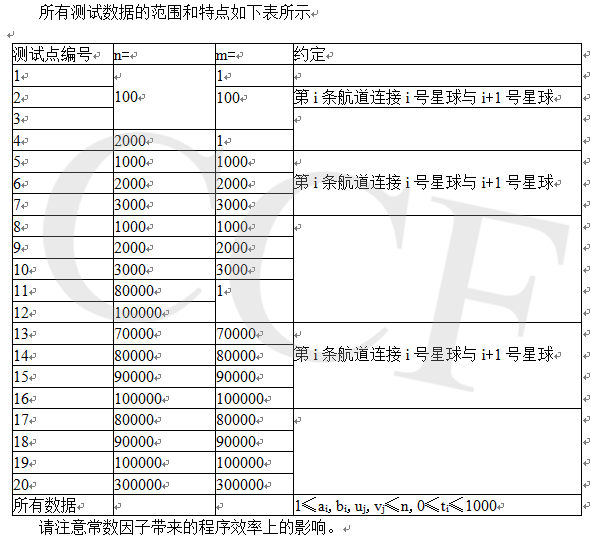
数据范围限制

限制

时间限制：\(1\texttt{s}\)
空间限制：\(256\texttt{MB}\)

来源

NOIP2015 提高组 Day2T3