题目描述

一条东西走向的穆西河将巴邻旁市一分为二，分割成了区域 A 和区域 B。

每一块区域沿着河岸都建了恰好 \(1,000,000,001\) 栋的建筑，每边的建筑都从 \(0\) 编号到了 \(1,000,000,000\)。相邻的每对建筑相隔 \(1\) 单位距离，河的宽度也是 \(1\) 个单位长度。区域 A 中的 \(i\) 号建筑物恰好与区域 B 中的 \(i\) 号建筑物隔河相对。

城市中有 \(N\) 个居民。第 \(i\) 个居民的房子在区域 \(P_i\) 的 \(S_i\) 号建筑上，同时他的办公室坐落在 \(Q_i\) 区域的 \(T_i\) 号建筑上。一个居民的房子和办公室可能分布在河的两岸，这样他就必须要搭乘船只才能从家中去往办公室，这种情况让很多人都觉得不方便。为了使居民们可以开车去工作，政府决定建造不超过 \(K\) 座横跨河流的大桥。由于技术上的原因，每一座桥必须刚好连接河的两岸，桥梁必须严格垂直于河流，并且桥与桥之间不能相交。

当政府建造最多 \(K\) 座桥之后，设 \(D_i\) 表示第 \(i\) 个居民此时开车从家里到办公室的最短距离。请帮助政府建造桥梁，使得 \(D_1 + D_2 + \cdots + D_N\) 最小。

输入

第一行，包含两个正整数 \(K\) 和 \(N\)，分别表示桥的上限数量和居民的数量。

接下来 \(N\) 行，每一行包含四个整数：\(P_i,S_i,Q_i,T_i\)，表示第 \(i\) 个居民的房子在区域 \(P_i\) 的 \(S_i\) 号建筑上，且他的办公室位于 \(Q_i\) 区域的 \(T_i\) 号建筑上。

输出

一行，包含一个整数，表示 \(D_1 + D_2 + \cdots + D_N\) 的最小值。

样例 1

输入

1 5
B 0 A 4
B 1 B 3
A 5 B 7
B 2 A 6
B 1 A 7

输出

24

样例 2

输入

2 5
B 0 A 4
B 1 B 3
A 5 B 7
B 2 A 6
B 1 A 7

输出

22

解释

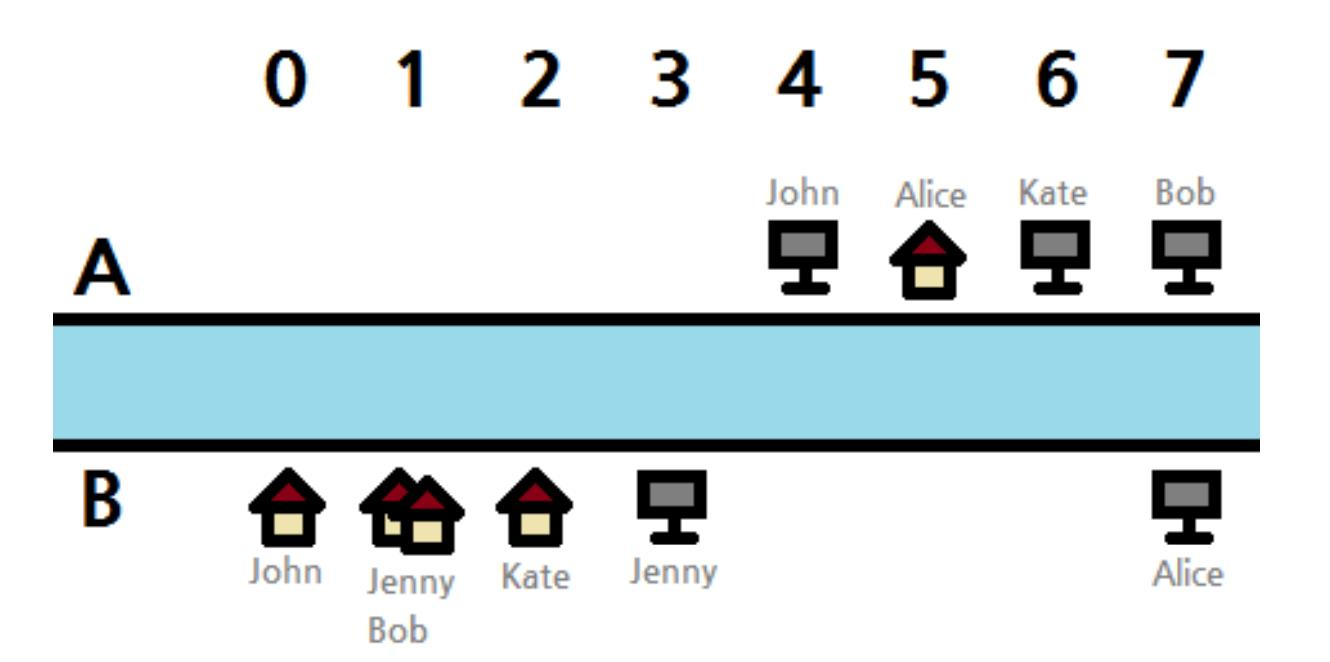
下图是两个样例输入的图示说明：

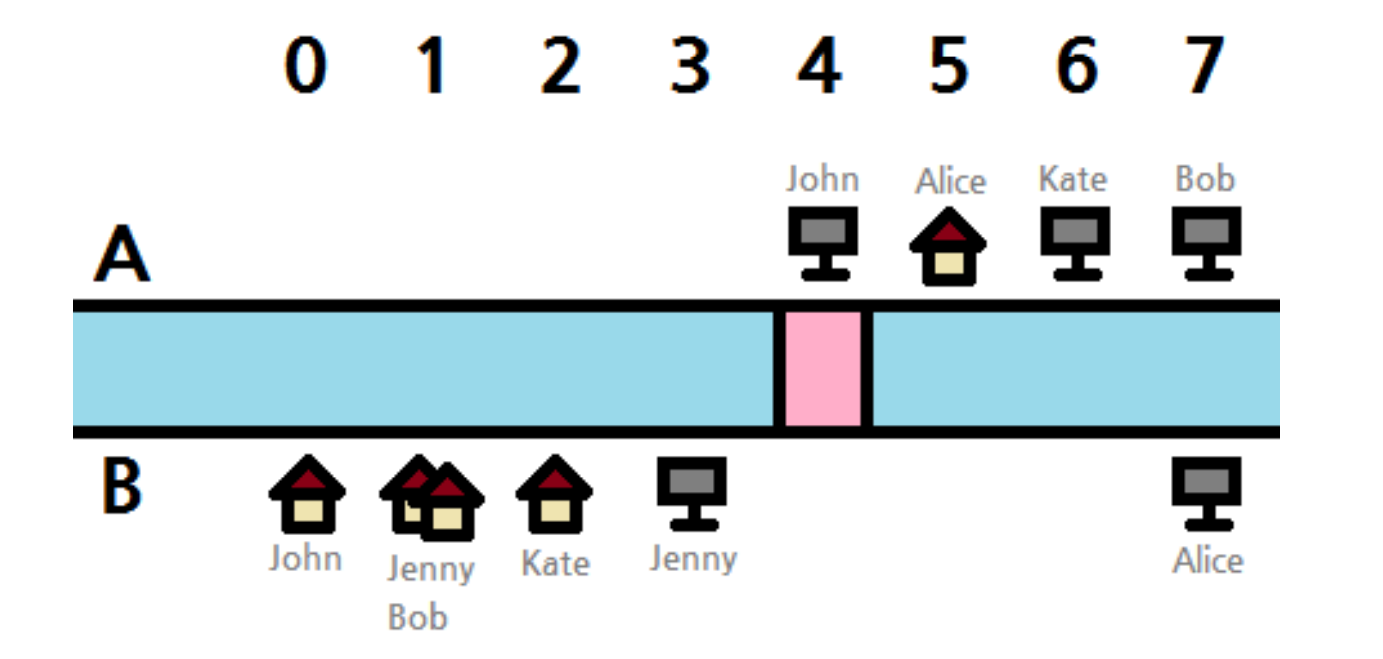
下面是样例 1 可能的一组最优方案，粉色的区域表示一座桥。

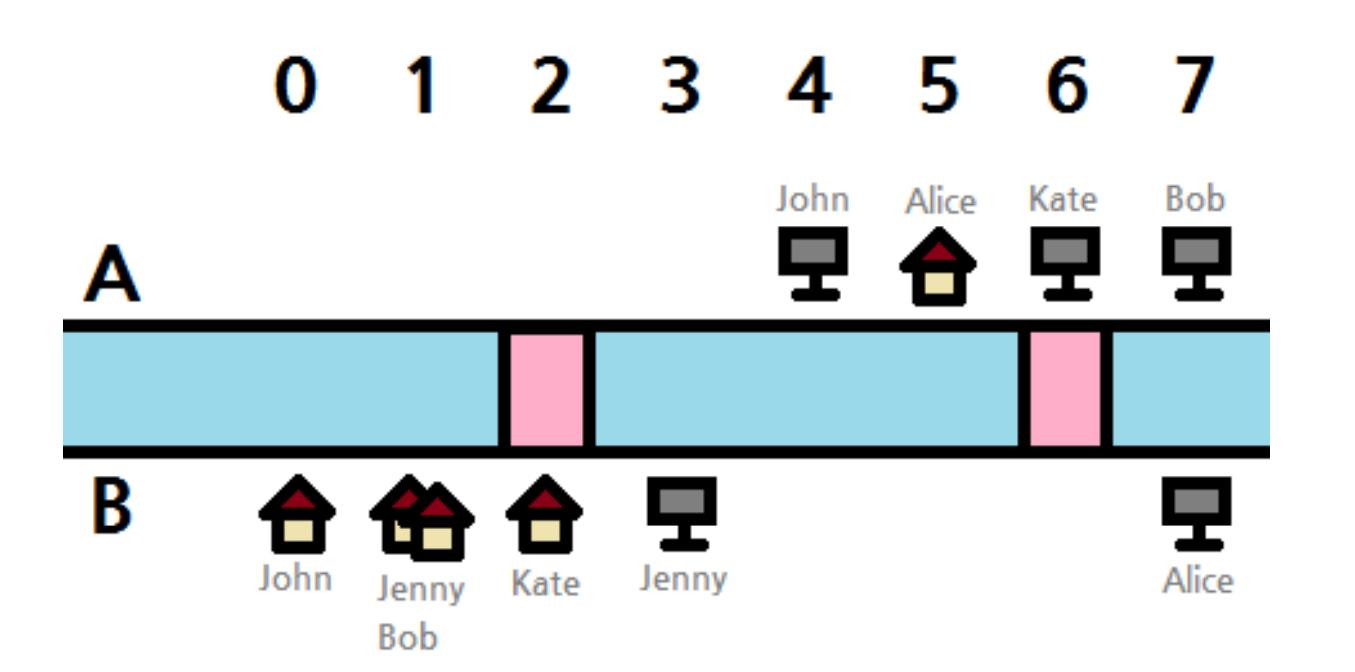
下面是样例 2 的一组可能的最优方案。

数据范围限制

共有五部分数据。

所有数据都保证：\(0 \leq S_i,T_i \leq 1,000,000,000\)，\(P_i\) 和 \(Q_i\) 为字符 A 和 B 中的一个，同一栋建筑内的可能有超过 1 间房子或办公室（或同时大于等于1）。

第 1 部分数据占8分，数据范围满足：\(K=1\)，\(1 \leq N \leq 10^3\)；
第 2 部分数据占14分，数据范围满足：\(K=1\)，\(1 \leq N \leq 10^5\)；
第 3 部分数据占9分，数据范围满足：\(K=2\)，\(1 \leq N \leq 10^2\)；
第 4 部分数据占32分，数据范围满足：\(K=2\)，\(1 \leq N \leq 10^3\)；
第 5 部分数据占37分，数据范围满足：\(K=2\)，\(1 \leq N \leq 10^5\)。

来源

APIO2015