暂无测试数据。

题目描述

组合子逻辑是 Moses Schönfinkel 和 Haskell Curry发明的一种符号系统，
用于消除数理逻辑中对于变量的需要。
本题考察一种与真实世界的组合子演算略有差别的组合子系统。
一个组合子项是下列形式之一：

 P
 (E1 E2)

其中 \(P\) 表示一个基本函数，
\(E1\) 以及 \(E2\) 表示一个组合子项(可以相同)。
不满足以上形式的表达式均非组合子项。

我们将一个组合子项E的参数个数 \(np(E)\) 如下：
np(P)=基本函数P的参数个数；
np((E1 E2))=np(E1)-1

本题中，
我们用一个正整数同时表示一个基本函数，
以及该基本函数的参数个数。

对于一个组合子项 \(E\)，
如果它和它包含的所有组合子项的参数个数 \(np\) 均为正整数，
那么我们称这个 \(E\) 为范式。

我们经常将组合子项简化表示：
如果一个组合子项E含有连续子序列(…((E1 E2)E3)…En)(其中\(n \geq 3\))，
其中 \(Ek\) 表示组合子项（可以是简化表示的），
那么将该部分替换为 (E1 E2 E3 … En)，其他部分不变，
得到表达式 E 的一个简化表示。
一个组合子项可以被简化表示多次。

给定一个基本函数序列，
问至少需要添加多少对括号，
才能使得该表达式成为一个范式的简化表示（即满足范式的性质）；
如果无论怎样添加括号，
均不能得到范式的简化表示，
输出-1。

输入

第一行，包含一个正整数 \(T\)，表示有 \(T\) 次询问。
接下来 \(2T\) 行。
第 \(2k\) 行有一个一个整数，表示第 \(k\) 次询问的序列中基本函数的个数。
第 \(2k+1\) 行有个正整数，其中第 \(i\) 个整数表示序列中第 \(i\) 个基本函数。

输出

输出 \(T\) 行，
每行一个整数，表示对应询问的输出结果。

样例输入

2
5
3 2 1 3 2
5
1 1 1 1 1

样例输出

3
-1

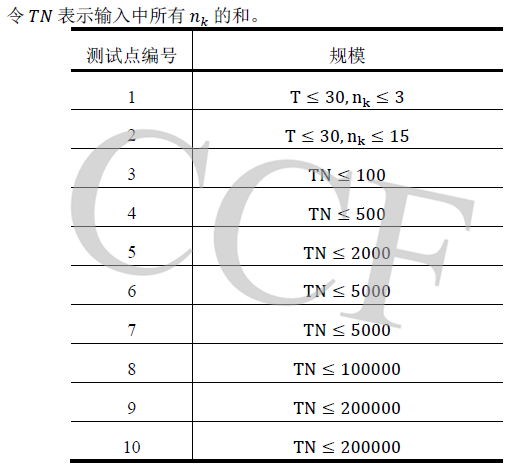
数据范围限制

限制

每个测试点时限：1秒
内存限制：128MB

来源

CTSC2013