暂无测试数据。

题目描述

通过代数基本定理，
我们知道若计算重根，
一个 \(n\) 次的多项式在复数域内恰好有 \(n\) 个零点(函数值为 0 的点)。

现给定一个整系数多项式 \(F[x]\)，
它的 \(n\) 个零点恰好都是有理数（即可以写成两个整数相除的形式）；
同时，
若我们把它所有的非零零点（函数自变量不为0，函数值为0）去重，
则可以得到 \(r\) 个互不相同的非零零点，
其中第 \(i\) 个非零零点可以被表示成下式：

\(\displaystyle sng_i* \frac{q_i}{p_i}\)

式中 \(sgn_i\) 表示第 \(i\) 个零点的符号，
\(p_i\) 和 \(q_i\) 为互质的两个正整数。

现在告诉你 \(F[x]\)，
要求你输出将它因式分解后的形式。

输入

只有一行，包含多项式 \(F[x]\)。

多项式一定是如下的形式：

\(a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0\)

次数一定为从高到低，
其中 \(a_i\) 为整数，
并且若 \(a_i\) 为 0，
则省略该项，
若 \(a_i\) 为负数，
则省略之前的加号，
若 \(a_i\) 的绝对值为 1 且 \(i\) 不为0，
则不输出1，
并且保证 \(a_n\) 不为 0。
详见样例输入。

输出

输出一行，
表示因式分解后的形式，
格式如下：

\(a_n(x+u_1/v_1)^{t_1} (x+u_2/v_2)^{t_2} \cdots (x+u_s/v_s)^{t_s}\)
其中 \(u,v\) 互质，且 \(v\) 为正整数。

其中 \(u_i/v_i=0\) 从小到大排列，
若 \(u_i/v_i=0\) 则该项为 \(x^{t_i}\)，
若 \(u_i/v_i\) 为负数，则省略加号，
若 \(v_i\) 为 1，则省略 \(/v_i\)。
若 \(t_i\) 为1，则省略 ^\(t_i\)。
若 \(a_n\) 为 \(\pm 1\), 则将 1 省略。

详见样例输出。

样例输入

8x^7-258x^5+2112x^3-512x

样例输出

8(x-4)^2(x-1/2)x(x+1/2)(x+4)^2

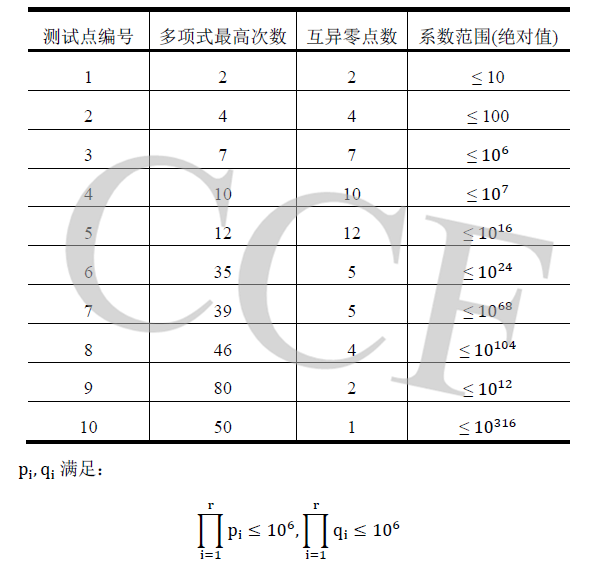
数据范围限制

限制

每个测试点时限：6秒
内存限制：512MB

来源

CTSC2013