暂无测试数据。

题目描述

小Q和小M最近发明了一种卡牌游戏，
叫猴子大战。

游戏最初小Q和小M各会获得一部分猴子牌。
每局游戏，
他们两个需要分别等概率地从自己的猴子牌中抽取一张进行战斗。
获胜的一方将获得双方的猴子牌。
如果一方获得了所有的猴子牌，
则该方获得整场游戏的胜利。
否则游戏将一直进行下去。

在进行了若干场比赛以后，
小Q和小M算出了一张胜率表，
为每两张猴子牌之间进行战斗双方获胜的概率。
由于每场战斗一定会决出胜负，
而且胜率不受先后顺序影响，
因此对于任意的两张猴子牌A和B，
A战胜B的概率加B战胜A的概率为 1。

由于自己老是输给小M，
小Q开始怀疑自己每次拿到的猴子牌是否能获得胜利。
他希望求出自己拿到的每种猴子牌组合的获胜的概率。

由于小Q接下来还有在CD市体育中心数以万计的运动计划，
因此这个问题只能交给你来解决了。

输入

第一行，包含两个正整数\(n\)和\(m\)，
表示猴子牌的总张数和需要求的猴子牌组合的个数。

接下来有 \(n\) 行，
每行包含 \(n\) 个实数，
每个实数保留了两位小数。
这 \(n\) 行中，
其中第 \(i\) 行第 \(j\) 列的数为 \(P_{i,j}\)，
表示第 \(i\) 张猴子牌战胜第 \(j\) 张猴子牌的概率。
保证 \(P_{i,j}+P_{j,i}=1\)。
特别地，\(P_{i,i}=0.5\)，没有特殊意义。

最后有 \(m\) 行。
每行包含一个长度为 \(n\) 的无空格分隔的 01 串，
表示一个猴子牌的组合。
其中第 \(i\) 个字符如果为 0，
表示最初第 \(i\) 张牌在小M处，
否则表示在小Q处。

输出

输出 \(m\) 行，
每行一个实数，
四舍五入保留八位小数，
依次表示每个给定的猴子牌组合下小Q获胜的概率。

样例输入

3 4
0.50 0.60 0.40
0.40 0.50 0.70
0.60 0.30 0.50
110
011
111
000

样例输出

0.71304348
0.66086957
1.00000000
0.00000000

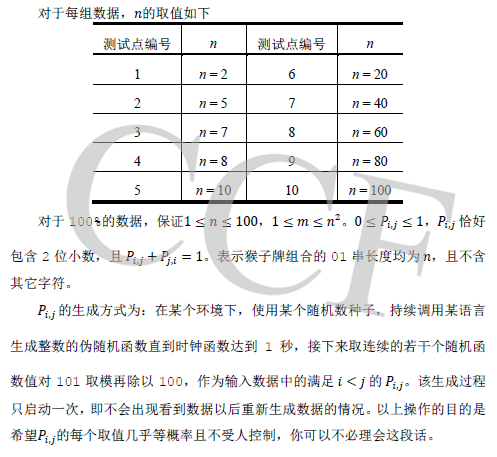
数据范围限制

限制

每个测试点时限：2秒
内存限制：256MB

来源

CTSC2013