1197. 紫荆花之恋
暂无测试数据。
题目描述
强强和萌萌是一对好朋友。
有一天他们在外面闲逛,
突然看到前方有一棵紫荆树。
这已经是紫荆花飞舞的季节了,
无数的花瓣以肉眼可见的速度从紫荆树上长了出来。
仔细看看的话,
这个大树实际上是一个带权树。
每个时刻它会长出一个新的叶子节点。
每个节点上有一个可爱的小精灵,
新长出的节点上也会同时出现一个新的小精灵。
小精灵是很萌但是也很脆弱的生物,
每个小精灵 \(i\) 都有一个感受能力值 \(r_i\),
小精灵 \(i,j\) 成为朋友当且仅当在树上 \(i\) 和 \(j\) 的距离 \(dist(i,j) \leq r_i + r_j\),
其中 \(dist(i,j)\) 表示在这个树上从 \(i\) 到 \(j\) 的唯一路径上所有边的边权和。
强强和萌萌很好奇每次新长出一个叶子节点之后,
这个树上总共有几对朋友。
我们假定这个树一开始为空,
节点按照加入的顺序从 1 开始编号。
由于强强非常好奇,
你必须在他每次出现新节点后马上给出总共的朋友对数,
不能拖延哦。
输入
共有 \(n+2\) 行。
第一行,包含一个正整数,表示测试点编号。
第二行,包含一个正整数 \(n\),表示总共要加入的节点数。
我们令加入节点前的总共朋友对数是 \(last_ans\),在一开始时它的值为 0。
接下来 \(n\) 行中第i行有三个数 \(a_i,c_i,r_i\),
表示节点 \(i\) 的父节点的编号为 \(a_i\ xor\) (last_ans mod \(10^9\) )
(其中 \(xor\) 表示异或,\(mod\) 表示取余,
数据保证这样操作后得到的结果介于 \(1\) 到 \(i–1\) 之间),
与父节点之间的边权为 \(c_i\),
节点 \(i\) 上小精灵的感受能力值为 \(r_i\)。
注意 \(a_1=c_1=0\),表示 1 号点是根节点,
对于 \(i > 1\),父节点的编号至少为 1。
输出
包含 \(n\) 行,
每行输出 1 个整数,表示加入第 \(i\) 个点之后,树上有几对朋友。
样例输入
0
5
0 0 6
1 2 4
0 9 4
0 5 5
0 2 4
样例输出
0
1
2
4
7
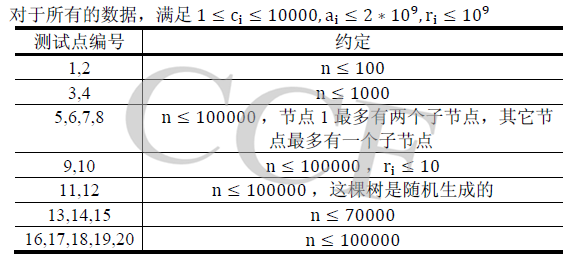
数据范围限制
限制
每个测试点时限:12秒
内存限制:512MB
来源
WC2014
信息
- ID
- 1196
- 难度
- (无)
- 分类
- (无)
- 标签
- (无)
- 递交数
- 0
- 已通过
- 0
- 通过率
- ?
- 上传者