1189. 随机数生成器
暂无测试数据。
题目描述
栋栋最近迷上了随机算法,
而随机数生成是随机算法的基础。
栋栋准备使用线性同余法(Linear Congruential Method)来生成一个随机数列,
这种方法需要设置四个非负整数参数 \(m,a,c,X_0\)
按照下面的公式生成出一系列随机数 \(<X_n>\):
\(X_{n+1} = (a X_n + c)\ mod\ m\)
其中 \(mod m\) 表示前面的数除以 \(m\) 的余数。
从这个式子可以看出,
这个序列的下一个数总是由上一个数生成的。
用这种方法生成的序列具有随机序列的性质,
因此这种方法被广泛地使用,
包括常用的 C++ 和 Pascal 的产生随机数的库函数使用的也是这种方法。
栋栋知道这样产生的序列具有良好的随机性,
不过心急的他仍然想尽快知道 \(X_n\) 是多少。
由于栋栋需要的随机数是 \(0,1,\cdots,g-1\) 之间的,
他需要将 \(X_n\) 除以 \(g\) 取余得到他想要的数,即 \(X_n\ mod\ g\),
你只需要告诉栋栋他想要的数 \(X_n\ mod\ g\) 是多少就可以了。
输入
6 个用空格分割的整数 \(m,a,c,X_0,n\) 和 \(g\),
其中 \(a,c,X_0\),是非负整数,\(m,n,g\) 是正整数。
输出
一个数,即 \(X_n\ mod\ g\)。
样例输入
11 8 7 1 5 3
样例输出
2
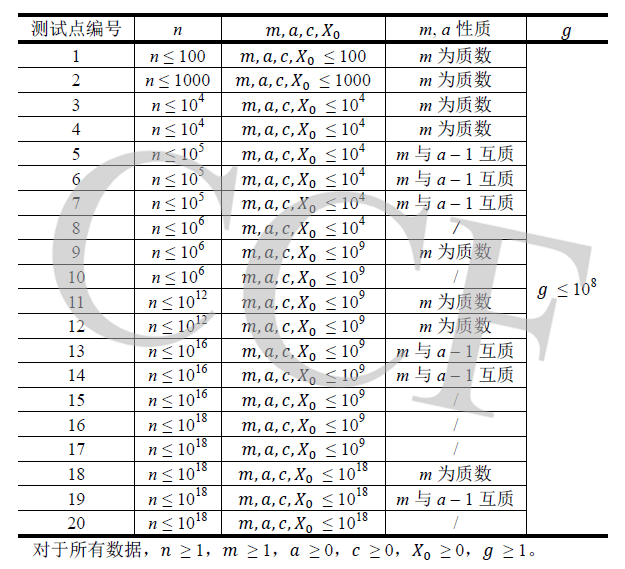
数据范围限制
来源
NOI2012
信息
- ID
- 1188
- 难度
- (无)
- 分类
- (无)
- 标签
- (无)
- 递交数
- 0
- 已通过
- 0
- 通过率
- ?
- 上传者