组合数问题
该比赛已结束,您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。
描述
题目大意
告诉你组合数公式
,其中n!=1*2*3*4*5*...*n;意思是从n个物体取出m个物体的方案数
现给定n、m、k,问在所有i(1<=i<=n),所有j(1<=j<=min(i,m))的(i,j)满足Cji(从i个数里选j个数的方案)是k的倍数
是k的倍数的个数。
格式
输入格式
第一行有两个整数t, k,其中t代表该测试点总共有多少组测试数据,k的意义见【问题描述】。
接下来t行每行两个整数n, m,其中n, m的意义见【问题描述】。
输出格式
t行,每行一个整数代表所有的0 <= i <= n, 0 <= j <= min(i, m)有多少对(i, j)满足Cji(从i个数里选j个数的方案)是k的倍数
样例1
样例输入1
1 2
3 3
Copy
样例输出1
1
Copy
样例2
样例输入2
2 5
4 5
6 7
Copy
样例输出2
0
7
Copy
限制
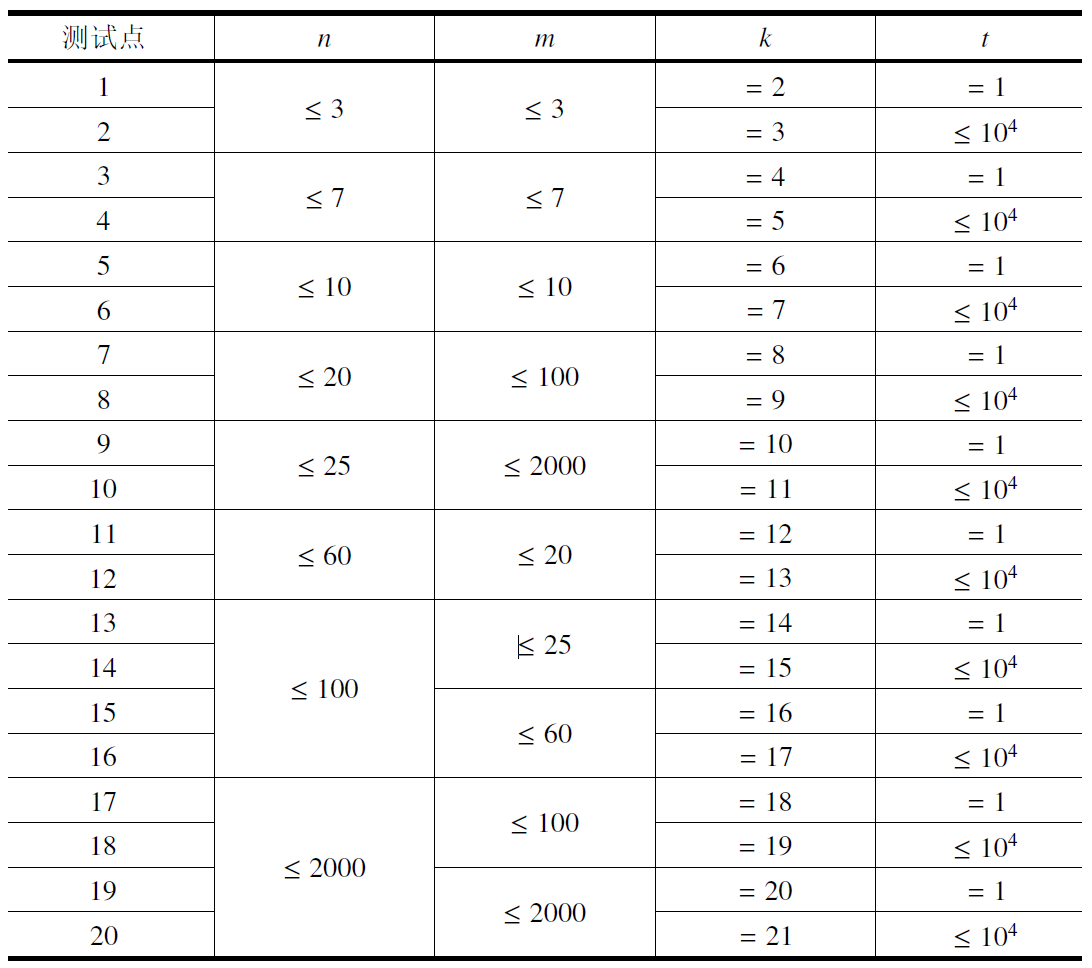
【子任务】
提示
【样例1说明】
在所有可能的情况中,只有C12是2的倍数