Description

Bernard有\(n\)个结点，编号\(1\)至\(n\)，一开始没有边。现在Bernard要新建\(m\)条边，构成一个图。每一条新建的边都是无向边。
但是要满足如下的条件：
1、选择两个不同编号的结点\(X\)和\(Y\)，在\(X\)和\(Y\)之间建立一条边，前提是两个结点的编号的差不超过给定的参数\(k\)，即\(0<x\)，\(y \leq k\)。 注意：允许在\(A\)和\(B\)之间建立多条边（即两个结点之间可以有重边）。
2、当最终建完\(m\)条边之后，对于任意的一个结点\(i\)，与结点\(i\)相连的边共有偶数条。 注意：\(0\)也被认为是偶数。
问：总共可以构造出多少种不同的图？答案对\(1000000007\)取模。
注意构出来的图可以是不连通的图。

Format

Input

一行，三个整数：\(n\)，\(m\)，\(k\)。

Output

一个整数，表示答案。

Sample 1

Input

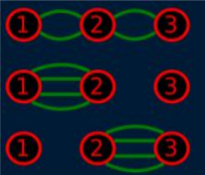
3 4 1

Output

3

Sample 2

Input

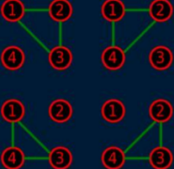
4 3 3

Output

4

Limitation

1s, 262144KiB for each test case.

Hint

样例解释1

样例解释2

对于\(100%\)的数据：\(1 \leq n \leq 30\)，\(0 \leq m \leq 30\)，\(1 \leq k \leq 8\)。