题目背景

某一天，fz20181223又在专心致志地建设祂的地铁，可某一天勘测地形时，祂发现邻村的绿绵羊蒟蒻因为没有软妹币只能造公交……于是，为了发扬人道主义精神对绵羊村进行铁路援助，fz20181223计划修一条高铁从藩镇到绵羊村。

题面描述

我们可以把fz20181223的地铁路线图和绿绵羊的公交路线图看作一个 \(n\) 个点 \(m\) 条边的图。这张图可以分成两个部分，这两个部分都是连通图，但互相不连通。给出这个图里每一条边的起点 \(x\) ，终点 \(y\) 和经过这一条边所需要的时间 \(w\) 。现在，你需要在这两个图之间新建一条边，长度为 \(f\) ，求连通后 需要最长时间的路线需要的最短时间 是多少。

输入输出格式

输入格式

第 \(1\) 行：两个数，代表 \(n\) 和 \(m\) 。
第 \(2\) ~ \(m+1\) 行：每行3个数，分别代表 \(x\) ， \(y\) ， \(w\)。
第 \(m+2\) 行：1个数，为 \(f\)。

输出格式

一行，一个数，代表高铁通车后需要最长时间的路线需要的最短时间是多少。

输入输出样例

输入样例#1

7 6
1 2 2
2 4 8
1 4 1
2 5 5
3 6 3
6 7 4
10

输出样例#1

19

说明

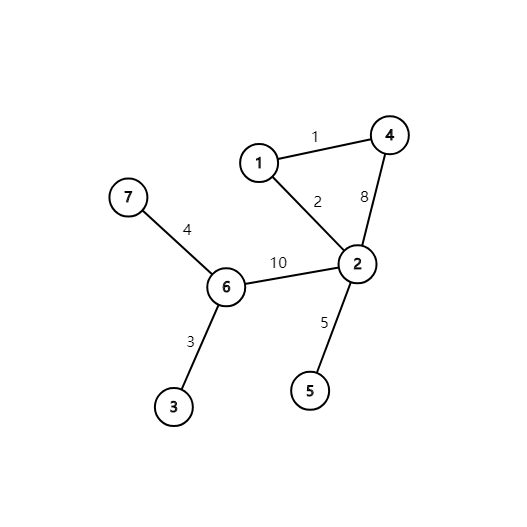
如图，连接 \(2\) 和 \(6\) ，在这种情况下需要最长时间的路线为7->6->2->5，需要时间为 \(19\) 。其他连接方法得出的结果均大于 \(19\) 。

---

对于 \(30\) %的数据， \(1\) ≤ \(n\) ≤ \(100\) ， \(1\) ≤ \(m\) ≤ \(1000\)
对于 \(60\) %的数据， \(1\) ≤ \(n\) ≤ \(300\) ， \(1\) ≤ \(m\) ≤ \(2000\)
对于另外 \(10\) %的数据，保证图两部分的形态都是菊花状，如这样：

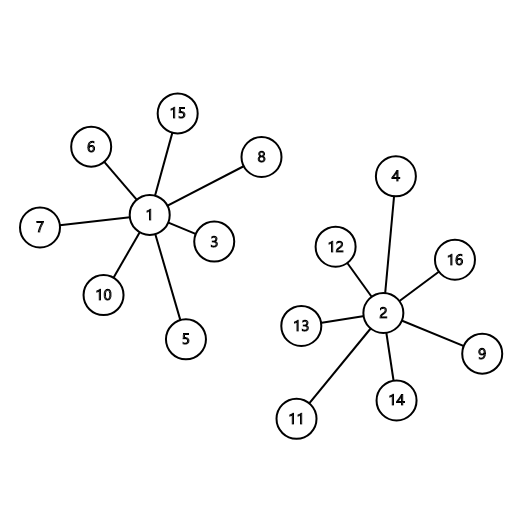
对于 \(100\) %的数据， \(1\) ≤ \(x\) , \(y\) ≤ \(n\) ≤ \(500\) ， \(1\) ≤ \(m\) ≤ \(6000\) ， \(1\) ≤ \(w\) , \(f\) ≤ \(1000\) 。
数据保证两个不连通部分点数的比值在 \(\frac{1}{3}\) 与 \(3\) 之间，简单来说，就是两个不连通部分中点数多的部分的点数不超过点数少的部分的点数的 \(3\) 倍。
另外，绿绵羊就是出题人limingyang的代号（不会把不会吧还有人不知道这个？）
而fz20181223正是本场比赛的凉心验题人之一哦~
\(\sout\texttt{fz20181223 : 公交真好van，我也要开车}\)

鸣谢

@fz20181223