数字华容道
该比赛已结束,您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。
背景
Zyq在何老板的淘宝店买了一个数字华容道。
描述
这个华容道方阵大小是 \(n \times n\) 的,其中有 \(1, 2, 3, \cdots, n^2 - 1\) 这 \(n^2 - 1\) 个数。
记这个方阵为 \(a\),则第 \(i\) 行第 \(j\) 列的数为 \(a_{i, j}\)。
这 \(n^2 - 1\) 个数在方阵上排列时会有一个空缺的格子(如图)。
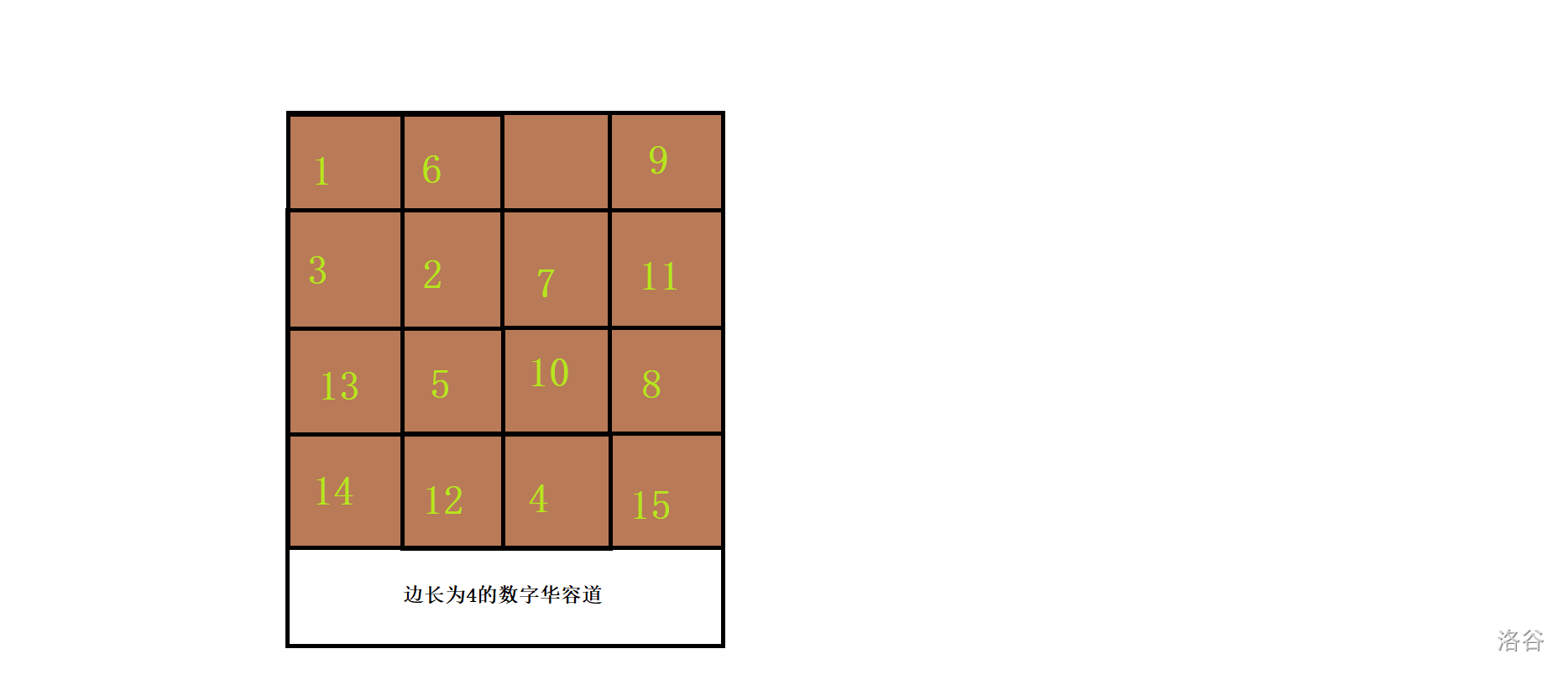
数字可以通过空缺的格子移动。
只能通过空缺的格子移,将与其相邻的格子移动到空缺的位置上。
移完后原数的位置成为新的空缺位置。
不能将数移出边界,也不能让同一格子有两个以上的数。
下面是一张移动的示意图:
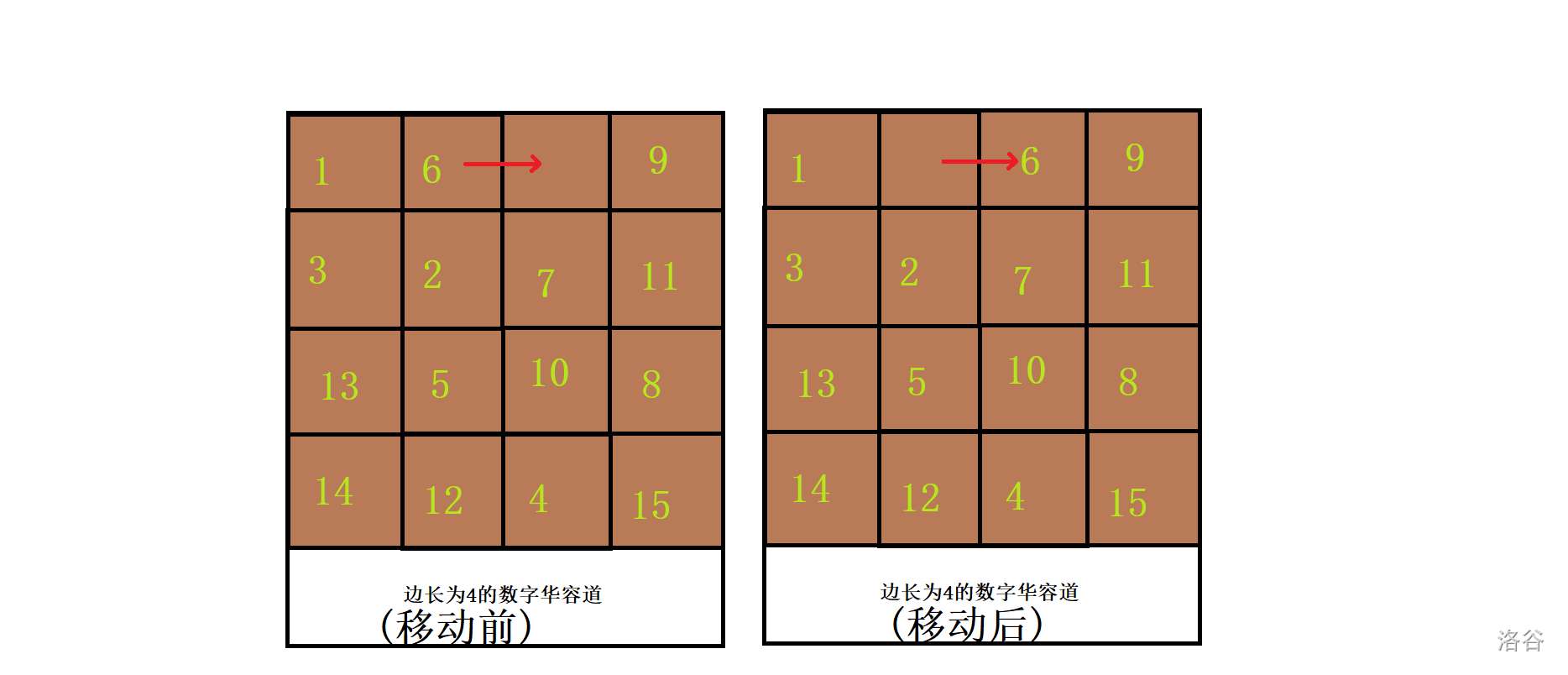
最终应该还原成如图所示的分布:
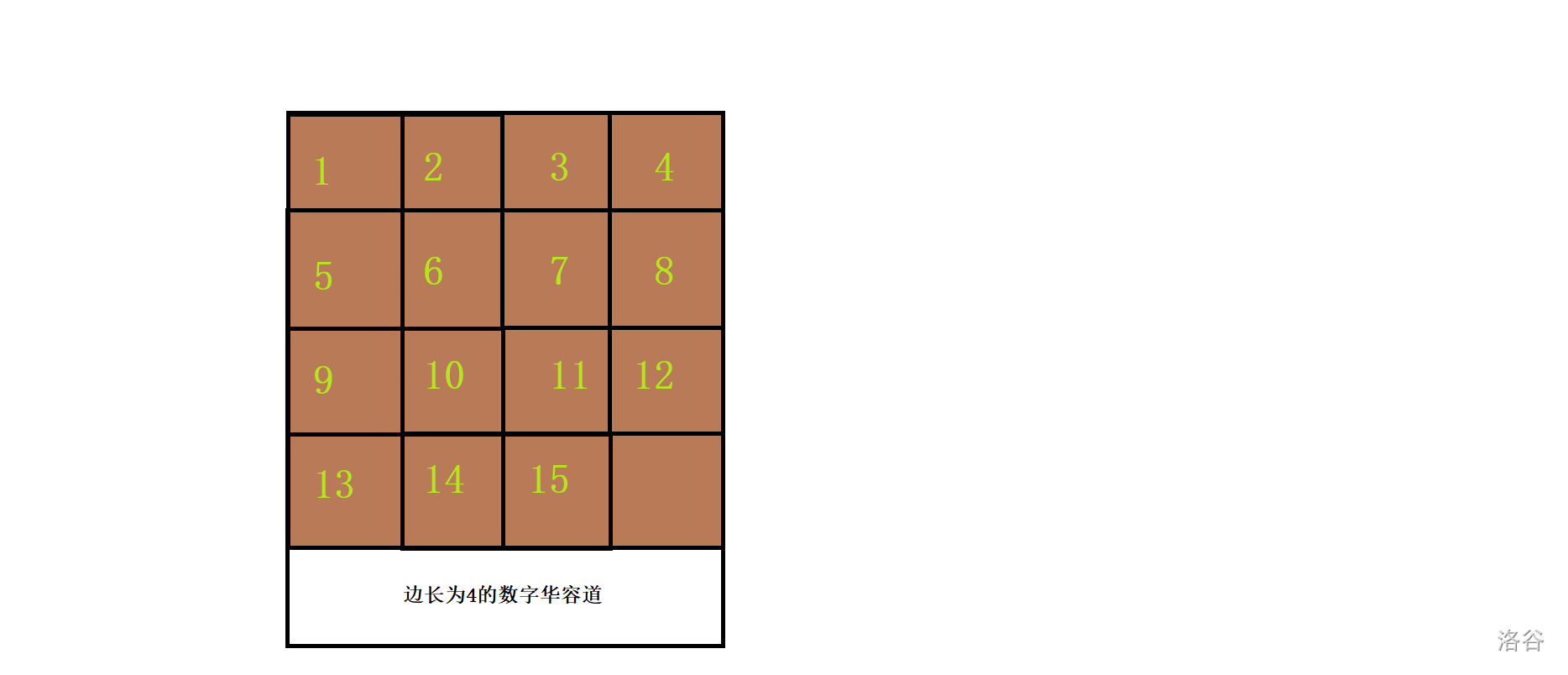
然而,不是所有的方阵都满足上述条件。
例如,将上图的 \(13\) 和 \(14\) 进行交换,得到的方阵无论如何都无法复原。
你的目标是求出能否在上述规则下使 \(\forall{i, j(1 \leq i \leq n, 1 \leq j \leq n, i + j < 2 \times n)},a_{i, j} = (i - 1) \times n + j - 1\)(即能否复原)。
格式
本题有多组数据
输入格式
第一行两个整数 \(T, n\),表示数据组数和方阵边长。
对于每组数据:
\(n\) 行,每行 \(n\) 个整数,表示初始的分布(空缺用 \(0\) 表示)。
输出格式
对于每组数据,输出一行字符串,如果可以还原,输出 YE5;否则输出 N0。
样例
样例输入#1
2 4
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 0
1 2 3 4
5 6 7 8
9 10 11 0
13 15 14 12
样例输出#1
YE5
N0
说明/提示
请务必注意输出内容!最好是复制粘贴!
对于 \(100\%\) 的数据,\(4 \le n \leq 1666\),\(1 \le T \leq 10\),保证
\(0, 1, 2, \cdots, n^2 - 1\) 都仅出现一次。
注:如果你想玩数字华容道,请点这里
【LZR-001】LZOJ 2020 年 6 月月赛 Div.2
- 状态
- 已结束
- 规则
- OI
- 题目
- 4
- 开始于
- 2020-06-12 18:00
- 结束于
- 2020-06-13 14:00
- 持续时间
- 20.0 小时
- 主持人
- 参赛人数
- 6