该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

题目背景

NOIP2018普及组第4题。

问题描述

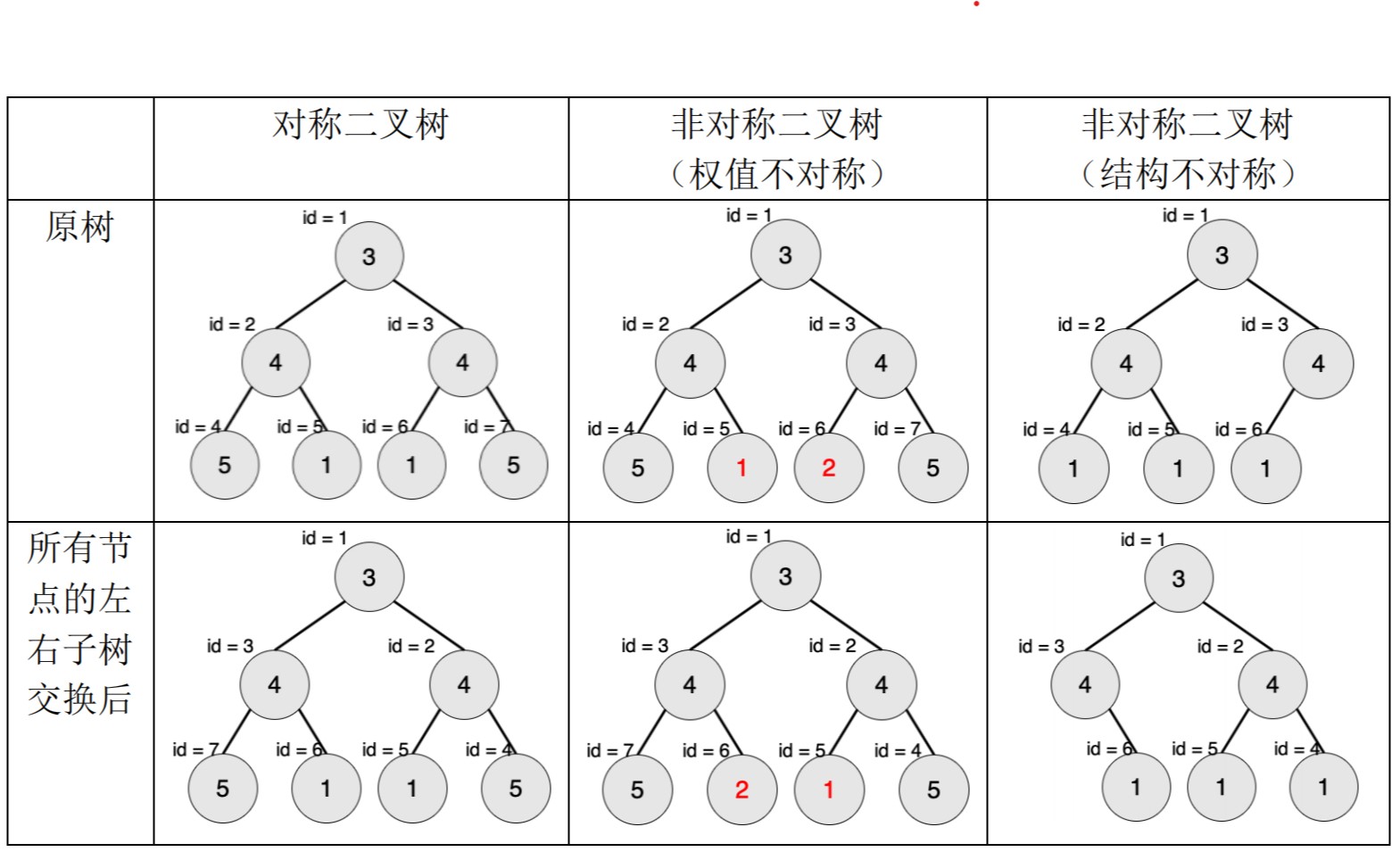
一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：

1.二叉树；

2.将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值，节点外的 id 表示节点编号。

现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数 最多。请输出这棵子树的节点数。

注意：只有树根的树也是对称二叉树。本题中约定，以节点 T 为子树根的一棵“子 树”指的是：节点T 和它的全部后代节点构成的二叉树。

输入格式

第一行一个正整数 n，表示给定的树的节点的数目，规定节点编号 1∼n，其中节点 1 是树根。

第二行 n 个正整数，用一个空格分隔，第 i 个正整数 vi代表节点 i 的权值。

接下来 n 行，每行两个正整数 li,ri，分别表示节点 i 的左右孩子的编号。如果不存在左 / 右孩子，则以 -1 表示。两个数之间用一个空格隔开。

输出格式

输出共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

样例数据

样例输入1

2 
1 3 
2 -1 
-1 -1 

样例输出1

1

样例输入2

10 
2 2 5 5 5 5 4 4 2 3 
9 10 
-1 -1 
-1 -1 
-1 -1 
-1 -1 
-1 2 
3 4 
5 6 
-1 -1 
7 8

样例输出2

3

提示

• 样例解释

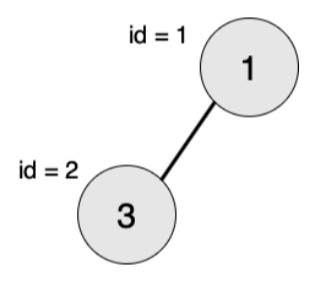
  【输入输出样例1解释】

  

  最大的对称二叉子树为以节点 2 为树根的子树，节点数为 1。

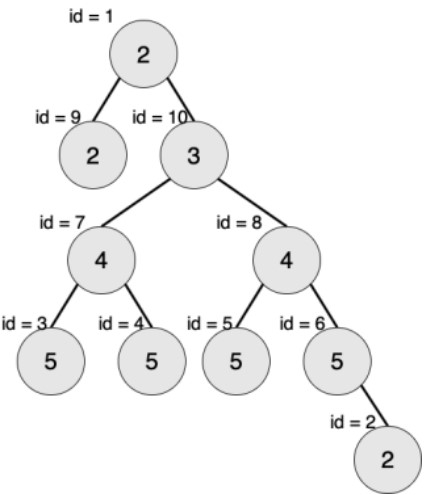
  【输入输出样例2解释】

  

  最大的对称二叉子树为以节点 7 为树根的子树，节点数为 3。

• 数据范围

  共 25 个测试点。

  vi≤1000。

  测试点 1∼3,n≤10，保证根结点的左子树的所有节点都没有右孩子，根结点的右子树
  的所有节点都没有左孩子。

  测试点 4∼8,n≤10。

  测试点 9∼12,n≤10^5，保证输入是一棵“满二叉树” 。

  测试点 13∼16,n≤10^5，保证输入是一棵“完全二叉树”。

  测试点 17∼20,n≤10^5，保证输入的树的点权均为 1。

  测试点 21∼25,n≤10^6。

• 约定

  层次：节点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一节点的层次等于其父亲节点的层次加 1。

  树的深度：树中节点的最大层次称为树的深度。

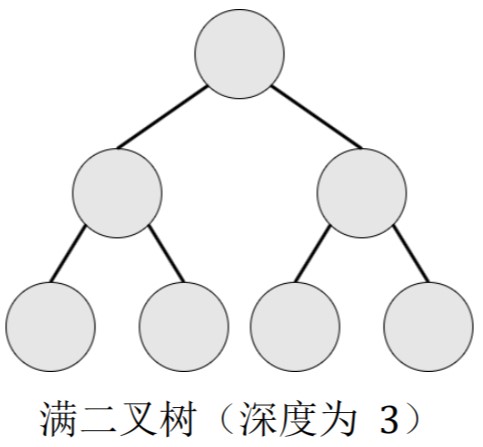
  满二叉树：设二叉树的深度为 h，且二叉树有 2h−1 个节点，这就是满二叉树。

  

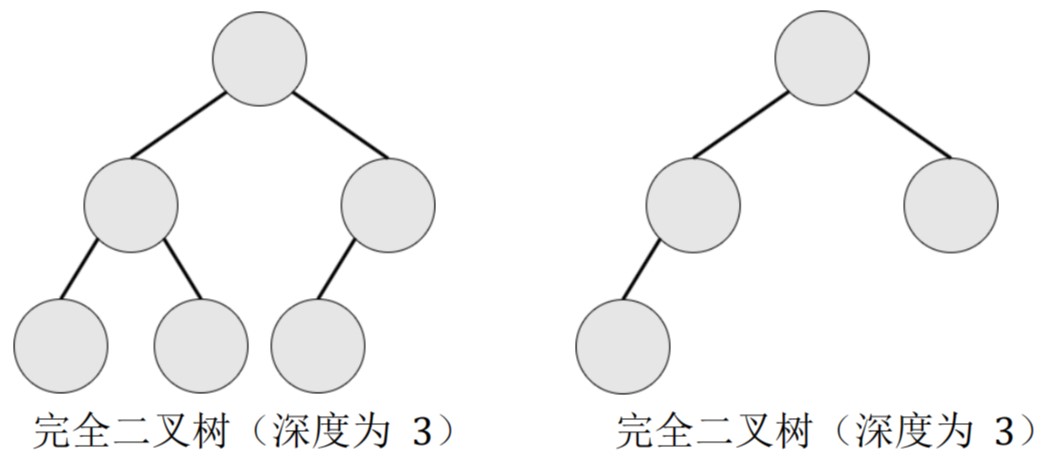
  完全二叉树：设二叉树的深度为 h，除第 h 层外，其它各层的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。