题目描述

给一棵树 n 个顶点，顶点编号为 0 - $n - 1$，以及一个数 m，树上的每条边都有一个权值（0 到 9 之间的整数），问有多少点对 (u, v) 使得 u 到 v 路径上的权值组成的数可被 m 整除（像字符串一样组成）。
例如：1 -> 2 : $w_1$, 2 -> 3 : $w_2$, …, i-1 -> i : $w_{i-1}$；
1 -> i : $w_1$$w_2$…$w_{i-1}$ ($\sum_1^{k-1}w_i \times 10^{k-1-i}$)

输入格式

第一行两个整数 n, m。
接下来 n - 1 行，每行三个整数 $u_i$, $v_i$, $w_i$，表示 $u_i$ 到 $v_i$ 有边权值 $w_i$ (0 $\leq$ $u_i$, $v_i$ < n)。

输出格式

输出满足条件的点对数。

样例1

输入

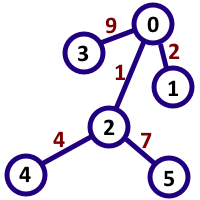
6 7
0 1 2
4 2 4
2 0 1
3 0 9
2 5 7

输出

7

样例2

输入

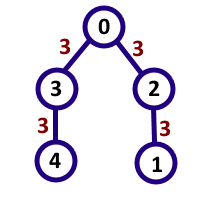
5 11
1 2 3
2 0 3
3 0 3
4 3 3

输出

8

数据范围

对于 30%的数据，2 $\leq$ n $\leq$ 50, 1 $\leq$ m $\leq$ 100, gcd(m, 10) = 1, 0 $\leq$ $u_i$, $v_i$ < n, 1 $\leq$ $w_i$ $\leq$ 9；
对于 100%的数据，2 $\leq$ n $\leq$ 100,000, 1 $\leq$ m $\leq$ $10^9$, gcd(m, 10) = 1, 0 $\leq$ $u_i$, $v_i$ < n, 1 $\leq$ $w_i$ $\leq$ 9。

限制

3s, 256M

样例解释

样例 1：点对：(0, 4), (1, 2), (1, 5), (3, 2), (2, 5), (5, 2), (3, 5)，组成的值：
14, 21, 217, 91, 7, 7, 917 ，共 7 对都整除 7。点对(2, 5) 和 (5, 2)是不同
的。

样例 2：点对：(4, 0), (0, 4), (3, 2), (2, 3), (0, 1), (1, 0), (4, 1), (1, 4)，组成
33 和 3333，共8 对都整除11.

来源

Codeforces716E
CWOI新高二专题测试十七