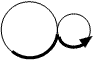Sunnypig闯穿梭关
测试数据来自 system/1086
背景
贪玩的sunnypig请Charles为他打造一个奇幻世界,Charles欣然答应了。然而一向善于出难题的Charles是决不会轻易让sunnypig轻松拥有一个奇幻世界的,于是Charles在建造过程中设置了重重机关,只有在sunnypig破解了这些障碍之后,才能尝试到奇幻世界中最有玩头的终极宝贝——时空穿梭机。虽然奇幻世界中其他的宝贝也很有趣,但贪玩的sunnypig怎能放过打boss的机会呢?于是他开始了破解障碍的旅程。
描述
第三道障碍是时空穿梭机的试用。
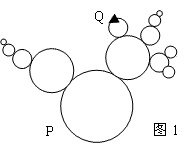
平面上有n个圆,其中一个半径为R0(R0=10^5)的圆,圆心处于坐标原点,它与若干个半径为R1的圆外切。每个半径为R1的圆与若干个半径为R2的圆外切……每个半径为Ri的圆与若干个半径为Ri+1的圆外切。任意两圆不相交、不重叠、不内含、不内切。半径为Ri的圆只可能与半径为Ri-1或Ri+1的圆外切,i>1时恰与一个半径为Ri-1的圆外切。在这些圆的边界上有若干个点对(Pi,Qi)。最开始,sunnypig在P1。如果sunnypig能从Pi沿着最短的光滑路径到达Qi的话,那么时空穿梭机便会将他传送到Pi+1,如此继续,直到他按此方式访问过所有的点(及如果从Pi到Qi时经过了Pj,则不算访问过Pj),才能算过关。
光滑路径是指:路径在两圆共切点拐弯时切线方向保持不变。图中左边两段(加粗)路径是光滑的,而右边的(加粗)路径不光滑。
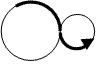

格式
输入格式
从标准输入中读取数据,文件第一行为3个整数n,m和t。其中1<=n,n+1<=m<=3000,1<=t<=100000,m表示圆的个数,并且圆的编号为1~m。t为特殊点的对数。50﹪的数据满足m<=300,t<=1000.第二行为n个正整数R1~Rn,并且当i>=1时有1<Ri<Ri-1-1。接下来的m行表示各个特殊点对,每行有4个数Xi,Yi,Si和Fi,(Xi,Yi)是圆i的圆心位置,圆i的半径是RSi,与圆i相切的尺寸更大的圆的编号是Fi,Xi和Yi可能是实数,并且X1=Y1=S1=F1=0。再接下来的t行表示各个特殊点对,每行有4个数PiW,PiA,QiW和QiA,用于描述一个特殊点对(Pi,Qi)的位置:PiW表示点Pi处于PiW这个圆上,并且以此圆圆心为原点,以从原点沿x轴正方向的半径为轴的幅角为PiA(0<=PiA<2π)。QiW表示点Qi处于QiW这个圆上,并且以此圆圆心为原点,以从原点沿x轴正方向的半径为轴的幅角为QiA(0<=QiA<2π)输入数据保证PiW≠QiW,任意特殊点不会同时处于两个圆上(即切点处无特殊点),并且一个圆最多与十个圆相切。
输出格式
标准输出中包含t行,其中第i行是一个整数Li,表示从点Pi到点Qi的最短光滑路径的长度/π后精确到整数的结果。
样例1
样例输入1
1 3 3
50000
0 0 0 0
150000 0 1 1
0 150000 1 1
3 5.497787 2 2.356194
3 1.570796 2 0.0
3 0.0 2 1.570796
样例输出1
175000
150000
200000
限制
各个测试点2s
不同测试点分数可能不同
提示
若需要arctan以外的反三角函数,又懒得自己编,可调用math单元,即在程序最开始(program 声明之后),加上一行"uses math;"即可。
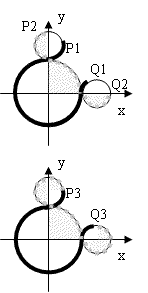
样例输入图片如下(not for measuring)
来源
湖南2005省队选拔赛
(原数据有误,建议不要用原数据调程序)